Introduction
Basic Equations
Goodness of Fit
Hypothesis Testing
Regression Diagnostics
Transformations
Alternative Methods for Linear Regression
References
The purpose of this section is to provide a brief overview of the equations and methods used in the analysis performed by this website. It is not intended to provide detailed explanations, derivations, or examples which can be found in most statistical text books. For professional use that may carry real world implementations or consequences, the use of a well established statistical software package is recommended for proper documentation.
Standard linear regression uses the method of ordinary least squares (OLS) to fit numerical data into the equation of a straight line by minimizing the sum of the squared vertical distances between observed data and a straight line. The minimization problem is solved using calculus from which an extensive list of mathematical expressions used in regression analysis is derived (Helsel and Hirsch, 2002). The method of least squares was first developed by the French mathematician Adrien-Marie Legendre (1752 - 1833).
The equation of a straight line can be expressed as y = a + bx, where a is the intercept with the y-axis and b is the slope of the line. Values of x are considered to be the independent or explanatory variable. Values of y are considered to be the dependent or response variable. In other words, the value of y depends on the value of x, but the value of x does not depend on the value of y.
The basic linear regression equations used in the analyses performed by this website are presented below. Some of the equations may take on a different form found in some statistical text books, the proof that they are equivalent is left as an exercise to the reader (real meaning, to complicated for me).
| No. | Equation | Explanation | Source |
|---|---|---|---|
| 1 | 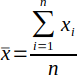 | Mean or average for x. | (Sanders, 1995) |
| 2 | 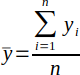 | Mean or average for y. | (Sanders, 1995) |
| 3 | 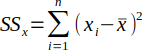 | Sum of the squares for x. | (Helsel and Hirsch, 2002) |
| 4 | 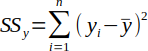 | Sum of the squares for y. | (Helsel and Hirsch, 2002) |
| 5 | 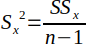 | Sample variance for x. | (Helsel and Hirsch, 2002) |
| 6 | 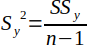 | Sample variance for y. | (Helsel and Hirsch, 2002) |
| 7 | 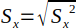 | Sample standard deviation for x. | (Helsel and Hirsch, 2002) |
| 8 | 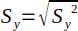 | Sample standard deviation for y. | (Helsel and Hirsch, 2002) |
| 9 | 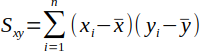 | Sum of the xy cross products. | (Helsel and Hirsch, 2002) |
| 10 | 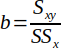 | Slope of the regression line. | (Helsel and Hirsch, 2002) |
| 11 | 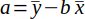 | Y-intercept of the regression line. | (Helsel and Hirsch, 2002) |
| 12 | 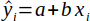 | Predicted value of y based on the regression line. | (Helsel and Hirsch, 2002) |
| 13 | 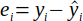 | Residual or difference between the observed and predicted value. | (Helsel and Hirsch, 2002) |
| 14 | 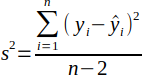 | Mean square error (MSE). | (Sanders, 1995) |
| 15 | 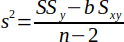 | MSE, alternate form according to Helsel et al. | (Helsel and Hirsch, 2002) |
| 16 | 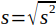 | Standard error or root mean square error (RMSE). | (Helsel and Hirsch, 2002) |
| 17 | 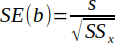 | Standard error of b (slope). | (Helsel and Hirsch, 2002) |
| 18 | 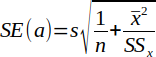 | Standard error of a (intercept). | (Helsel and Hirsch, 2002) |
| 19 | 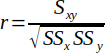 | Correlation Coefficient (Pearson's r). | (Helsel and Hirsch, 2002) |
| 20 | 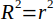 | Coefficient of determination. | (Helsel and Hirsch, 2002) |
| 21 | 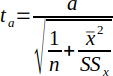 | Y-intercept test statistic used in hypothesis testing. | (Helsel and Hirsch, 2002) |
| 22 | 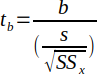 | Slope test statistic used in hypothesis testing. | (Helsel and Hirsch, 2002) |
| 23 | 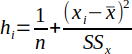 | Leverage in the x direction. | (Helsel and Hirsch, 2002) |
| 24 | 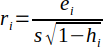 | Standardized residual (or internally studentized residual). | (Helsel and Hirsch, 2002) |
| 25 | 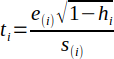 | Studentized residual. The symbol (i) denotes a deleted residual. | (Helsel and Hirsch, 2002) |
| 26 | 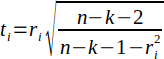 | Studentized residual, alternative form according to Fox. | (Fox, 2015) |
| 27 | 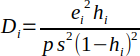 | Cook's Distance (Cook's D). | (Helsel and Hirsch, 2002) |
| 28 | 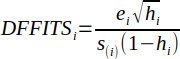 | Difference in Fits (DFFITS). | (Helsel and Hirsch, 2002) |
| 29 | 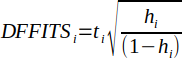 | DFFITS, alternative form according to Fox. | (Fox, 2015) |
| 30 | 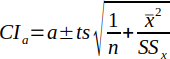 | Upper and Lower Confidence Interval for the intercept. t is the student's t-distribution such that t(α/2, n-2). | (Helsel and Hirsch, 2002) |
| 31 | 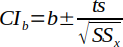 | Upper and Lower Confidence Interval for the slope. t is the student's t-distribution such that t(α/2, n-2). | (Helsel and Hirsch, 2002) |
| 32 | 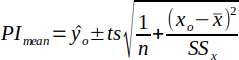 | Upper and Lower Prediction Intervals about the mean. t is the student's t-distribution such that t(α/2, n-2). | (Helsel and Hirsch, 2002) |
| 33 | 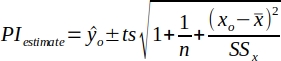 | Upper and Lower Prediction Intervals for the estimate. t is the student's t-distribution such that t(α/2, n-2). | (Helsel and Hirsch, 2002) |
There are various statistical measures to describe how well the regression model fits the data. These measures can be useful when comparing various transformation methods for a set of data. There are no specific cutoff values to describe a "good fit".
The mean square error (MSE) is calculated by Equation 14. MSE is the variance of the residuals, which is the measure of the average squared difference between the estimated values and the actual values. Smaller values indicate less error and a value of zero would indicate a perfect fit.
The standard error or root mean square error (RMSE) is calculated by Equation 16 and is the standard deviation of the residuals. Smaller values indicate less error and a value of zero would indicate a perfect fit.
Standard error of the slope (SE(b)) is the standard deviation of the slope and is calculated by Equation 17.
Standard error of the intercept (SE(a)) is the standard deviation of the intercept and is calculated by Equation 18.
The correlation coefficient (r) often referred as Pearson's r is calculated by Equation 19. It is a measure of how strong a relationship is between two variables. The closer r is to ±1, the better the correlation is between the variables. The closer r is to 0, the poorer the relationship is is between the variables.
The coefficient of determination (R2) is the square of the correlation coefficient (Equation 20). It is one of the most used measures to determine how strong a relationship is between two variables. The range of R2 is 0 to 1 and values closer to 1 indicate a better fit.
The width of the confidence intervals (CI) and prediction intervals (PI) provides a measure of the overall quality of the regression analysis. A narrower width indicates a better fit. Confidence intervals provide the range of a statistical parameter and prediction intervals provide the range where a predicted individual observation will fall at a specified confidence level. This website sets confidence levels at 95% (α = 0.05) using a two tailed student's t-distribution such that t(α/2, n-2) for confidence and prediction intervals.
Confidence intervals for the slope and intercept are calculated using Equations 30 and 31. Of a particular interest is if zero is in the range of the calculated CI's (see Hypothesis Testing).
Prediction intervals for the mean of Y at a given value of X due to the uncertainty of the true slope and intercept is calculated by equation 32 and is depicted by the red dashed lines in the Prediction Intervals plot. Prediction intervals for an individual estimate of y is calculated by equation 33 and is depicted by the blue dashed lines in the Prediction Intervals plot. If a transformation is used, the Prediction Intervals plot also shows the resulting regression line and transformed data which will help determine if linearity is acheived through the transformation.
Hypothesis testing can be used to determine if a relationship exists between X and Y in order to accept or reject the regression model. Two hypothesis tests commonly used in linear regression is to test whether the slope differs from zero and whether the intercept differs from zero.
Hypothesis testing can use the following seven-step procedure (Sanders, 1995):
1. Formulate the null and alternative hypothesis.
2. Select a level of significance.
3. Determine the test distribution to use.
4. Define the critical regions.
5. State the decision rule.
6. Compute the test ratio.
7. Make the statistical decision.
For linear regression with only one explanatory variable, the test for zero slope can determine if the value of y does vary as a linear function of x, or if the regression model has statistical significance.
1. The null hypothesis is H0: b = 0, and the alternative hypothesis Ha: b ≠ 0
2. A level of significance of α = 0.05, is commonly used, other levels can be selected as appropriate.
3. A students t-distribution will be used for linear regression hypothesis testing for analysis on this website.
4. The critical region (P-Value) will be probability of the test ratio (T-Ratio) using a two-tailed t-statistic with n-2 degrees of freedom.
5. The decision rule is to reject H0 and accept Ha if |P-Value| < α. Otherwise accept H0.
6. The test ratio (T-Ratio) for slope is given by Equation 22, which is the slope of the regression line divided by its standard error.
7. Make the statistical based on the decision rule decision to either reject H0 and accept Ha meaning that a linear correlation exists, or accept H0 meaning that a linear relationship does not exist.
The general consensus from many statisticians is that the intercept should not be dropped from a regression model or forcing the intercept to equal zero, even if the physical basis of data suggests that Y = 0 when X = 0. Knowing that the true population has to pass through the origin may not be a sufficient reason to force the sample population through the origin.
The hypothesis test for the intercept is almost identical to the slope test. The null hypothesis is H0: a = 0, and the alternative hypothesis Ha: a ≠ 0. The T-Ratio is is given by Equation 23, which is the intercept of the regression line divided by its standard error.
Regression diagnostics is used to identify points that could be potential outliers that may strongly influence the regression results. Although there are various recommended threshold or cutoff values for standard analysis set by mathematicians, knowing your data and if a result is reasonable is far more important.
Simply deleting a data point because it has been identified as a potential outlier may not always be appropriate. It's better to examine the source of the data to see if there was an error that could be corrected or if some unusual condition was present that could of affected the measured value, before considering deleting an outlier. Outliers should only be deleted if it strongly affects the regression results and if the point appears to be unreasonable. Your own expertise, intuition and judgment should be the ultimate decision maker for deleting an outlier from the analysis.
Versus Fits is a plot of residuals on the Y-Axis and fitted values on the X-Axis. The plot can be used to detect non-linearity and outliers. Versus Fits for a good model should resemble a scatter plot without any noticeable patterns or relationships.
Leverage is a measure of an outlier in the x direction and is calculated using Equation 23. Helsel suggests that a high leverage point is when hi > 3p/n, where p is the number of coefficients in the model (Helsel and Hirsch, 2002). For linear regression, p = 2 (slope, intercept). A point with high leverage that falls far from the regression line could exert a strong influence on the slope of regression line. A high leverage point alone does not necessarily make it an outlier.
Standardized residuals are is calculated using Equation 24. Helsel suggests that a point may be an outlier if |ri| > 3 (Helsel and Hirsch, 2002).
Studentized residuals can be calculated using Equation 25. The symbol (i) denotes that the ith residual is left out of the calculation (deleted residual). The calculation involves leaving out the ith data point and re-computing the regression statistics using the remaining data points. The procedure is repeated for each data point.
Fox presents an alternative method (Equation 26) that allows the studentized residuals be calculated without performing a separate regression analysis for each ith observation.
Some statisticians set the outlier threshold at |ti| > 3 and while others set the outlier threshold at |ti| > 2.
Studentized residuals should follow the t-distribution with n-p-1 degrees of freedom with p = 2 for linear regression (Helsel and Hirsch, 2002). This website sets the potential outlier threshold at the 95th confidence level (0.05 significance level) using a two-tail t-distribution such that |ti| > t0.05. For the case when n = 3 (n-p-1 = 0), the outlier threshold is defaulted to 12.706, which is the value when n = 4, although the studentized residuals will approach 0 with only 3 data points.
Cook's distance is calculated by Equation 27 and is one of the most widely used measures of influence (Helsel and Hirsch, 2002). Helsel suggests that a point may be an outlier based on the f-distribution such that Di > f0.1 (p+1, n-p).
Difference in Fits (DFFITS) can be calculated using equation 28 with deleted ith observations. Fox provides an alternative method (Equation 29) without performing a separate regression analysis for each ith observation (Fox, 2015).
Fox suggests that a point may be an outlier such that |DFFITSi| > 2√p/(n-p) with p = 2 (Fox, 2015).
A Q-Q plot is a graphical tool to help assess if the residuals (errors) are normally distributed, which is one the assumptions of the linear regression model. The theoretical percentiles for the normal distribution versus the observed sample percentiles of the residuals should plot as being linear. A Q-Q plot can also help to identify potential outliers.
Sample quantities are the ordered residuals from low to high. There are a different formulas to determine the percentile of the ordered residuals based on its rank (i). Theoretical quantities is the Z-score for the percentiles. The analysis for this website uses the following formulas for the percentile:
n ≤ 10, p = (i - 0.375) / (n + 0.25)
n > 10, p = (i - 0.5) / n
The line on the graph is drawn through the 25th and 75th percentiles.
"To transform or not to transform, that is the question."
Data that appears nonlinear but approximates some type of curve can often achieve linearity through variable substitution or through an appropriate transformation. It should be noted that diagnostics statistics is based on the substituted or transformed data, not the original data. For more involved transformations, the intercept (a) and/or the slope (b) must also be transformed back in the final form of the equation or model.
For simple variable substitution, the general equation is:
y = a + b[f(x)]
y = a + bx′ where x′ = f(x)
For simple functions that not on this site, you could transform the data prior to the analysis and use the results to determine if linearity is achieved or use the Quick Plot™ function on this site to see if the transformed data appears linear prior to analysis. Transformations available on this site that use simple variable substitution include:
y = a + b√x
y = a + b/x
y = a + blog(x)
y = a + bln(x)
y = a + bx2
The remaining transformations available on this site will be explained in more detail. For transformation involving logarithms, the following properties are used:
log(a*b) = log(a) + log(b)
log(ab) = b*log(a)
ln(e) = 1 or ln(ex) = x
y = (a + bx)2
Taking the square root on both sides of the equation results in √y = a + bx, which is now linear. The analysis
makes the substitution y′ = √y.
y = aebx
This is the classic exponential equation and is used extensively in modeling first order kinetics. Taking the natural log
of both sides of the equation and simplifying achieves a linear expression.
y = aebx
ln(y) = ln(aebx)
ln(y) = ln(a) + ln(ebx)
ln(y) = ln(a) + bx
The analysis makes the substitution y′ = ln(y). The calculated intercept (a′) must be transformed back such that a = ea′ into the final exponential form of the equation.
y = abx
Taking the log (base 10) of both sides of the equation and simplifying achieves a linear expression. Taking natural logs would also
result in the same regression line.
y = abx
log(y) = log(abx)
log(y) = log(a) + log(bx)
log(y) = log(a) + xlog(b)
The analysis makes the substitution y′ = log(y). The calculated intercept (a′) and slope (b′) must be transformed such that a = 10(a′) and b = 10(b′) into the final original form of the equation..
y = axb
Last but certainly not least, is the classic power equation which is also used often in modeling. Taking the log (base 10) of
both sides of the equation and simplifying achieves a linear expression.
y = axb
log(y) = log(axb)
log(y) = log(a) + log(xb)
log(y) = log(a) + blog(x)
The analysis makes the substitution y′ = log(y) and x′ = log(x). The calculated intercept (a′) must be transformed back such that a = 10a′ into the final power form of the equation.
Although the method of ordinary least squares (OLS) is the most well known method, there are other alternative methods that may be better suited for fitting certain types of data. The alternative methods predict different values for slope, which changes the overall characteristics regression line. Select methods for linear regression methods are described below.
The method of ordinary least squares (OLS) minimizes the sum of the squared vertical distances (Y on X) from the observed values to the fitted line. This method is best suited when values of Y are truly dependent on X. As example, first order kinetics such as radioactive decay, is truly dependent on time (time is plotted on the X-axis).
Instead of minimizing the squared vertical distances, OLS (X on Y) minimizes the squared horizontal distances from the observed values to the fitted line. This may be applicable when values of X are dependent on Y.
It is my recommendation that when this is the case, that values are switched (X->Y, Y->X) in order to maintain consistency with standard mathematical practice where Y is dependent on X. Although this method is included as an analysis option on this website for informational purposes, regression diagnostics will be supressed.
The line of organic correlation (LOC) minimizes the areas of the right triangles from the observed values to the fitted line, thus minimizing the errors in both the X and Y directions. This method is best suited for correlating data when X and Y are independent from each other, such as correlating daily stream flows on two different creeks.
Least normal squares (LNS) minimizes the squared perpendicular (normal) distance from the observed values to the fitted line. This method is best suited for physical locations, such as longitude and latitude.
| Method | Minimizes | Slope | Source |
|---|---|---|---|
| OLS | 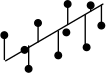 | 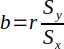 | (Helsel and Hirsch, 2002) |
| OLS(X on Y) | 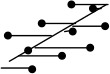 | 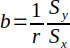 | (Helsel and Hirsch, 2002) |
| LOC | 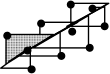 |  | (Helsel and Hirsch, 2002) |
| LNS | 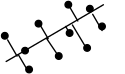 | 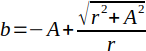 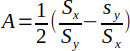 | (Helsel and Hirsch, 2002) |
Fox, John. Applied Regression Analysis and Generalized Linear Models, Third Edition. Thousand Oaks, California: SAGE Publications, Inc, 2015.
Helsel, D.R. and R. M. Hirsch. Statistical Methods in Water Resources, Techniques of Water Resources Investigations, Book 4, Chapter A3. Washington, DC.: U.S. Geological Survey, 2002.
NIST/SEMATECH. Engineering Statistics Handbook. Washington, DC.: U.S. Department of Commerce, 2012.
Sanders, Donald H. Statistics: A First Course, Fifth Edition. New York, New York: McGraw-Hill, Inc, 1995.